La nuova BBS è in fase Alpha. I post precedenti al 22 luglio 2024 potrebbero non essere trasferibili, ma rimarranno disponibili per la lettura su /old/.
@schappi@brotka.st do u know anything at all about the lie derivative vs covariant derivative discourse ?
-
@fiore I don't really know a source for it that I can recommend since this is a complex topic but I think the fundamental different that is worth to keep in mind is that the Lie derivative only cares about the topology of the space (so, the overall shape), whereas the covariant derivative/connection also cares about the geometry of the space (the distances between points, the angles between lines, the areas...).
For example, you can define a torus as a piece of papers with 1D portals on the sides. The Lie derivative will not change regardless of whether you consider a donut or a square with portals. But if you want to consider a connection, it will be different in both cases.
Another way to see it is with physics and circular paths. When you are moving in circles with a certain speed, then you have both a "linear" acceleration (the one that pushes you forward) and a "centripetal" acceleration (the one that makes you turn, preventing you from escaping the circular path). The "linear" accel. is the covariant derivative of your speed.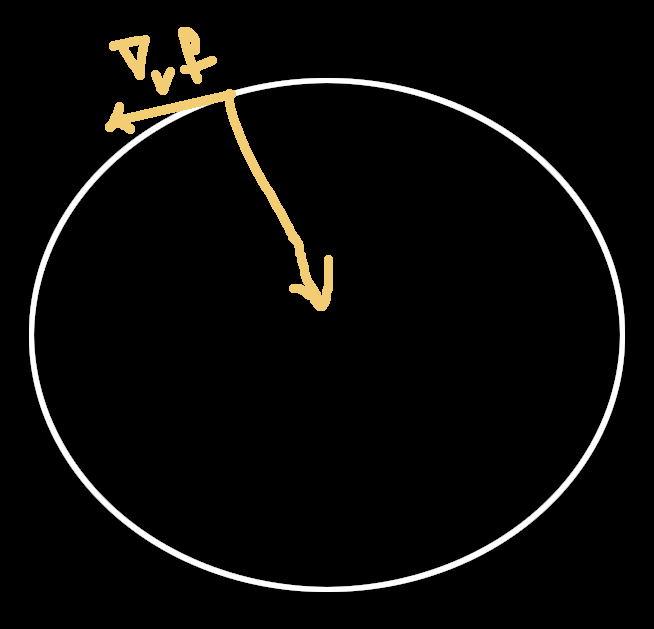
-
@fiore In a very crude way, the covariant derivative is the one that ignores what is happening outside of the space you are in, whereas the Lie derivative takes everything into account. -
@schappi@brotka.st mhmmmm okok i kinda see it .. basically you need a metric to know what a covariant derivative is ?
also , is it fair to say that uhm . this isnt very formal but . is it ok to say that the covariant derivative is the one that takes into account the """length""" of your vector , while the lie derivative doesnt ? (since it doesnt require a metric manifold to be defined )
-
@fiore yes, in fact you have a formula that relates the covariant derivative and the metric:
D_v g(X,Y)=g(CD_v X,Y)+g(X, CD_v Y)
where CD is the covariant derivative and D_v is the "regular" derivative (which only really works for functions).
afaik there is no formula like this for the lie derivative -
@schappi@brotka.st thats pretty cool ^^ thx !! (im doing GR and well its very interesting but sometimes the more abstract stuff flies away from me teehee )
-
@fiore oh ok since you are doing GR then I can tell you the more general version lol one nice thing about the lie derivative is that it extends very nicely to the more general case of tensor fields (because the Lie derivative is basically taking the pullback of a flow and you can write that in coordinates), though the covariant derivative has a bit of a nasty expression where you need to take the action of the vector field and then do the covariant derivative fo each component in the input... -
@fiore The downside of the Lie derivative is that yeah, it is *just* the directional derivative. Think of how the directional derivative of f from Calc 2 doesn't involve the dot product at all, you just kind of take the 1D derivative of f along the line x+tv... -
i didn't expect to learn and vaguely understand what a Lie derivative was today when i opened fedi
-
-
